
SQLITE NOT INSTALLED
Дальнобойная винтовка появилась в 19-ом веке спустя почти сто лет после того, как Даниил Бернулли опубликовал свою работу «Гидродинамика». В ней он показал связь между давлением и потенциальной энергией (или скоростью) жидкости. Использование этого принципа совместно с эффектом Вентури, связывающим увеличение скорости жидкости с уменьшением площади поперечного сечения, даёт ключ к пониманию баллистики снарядов.
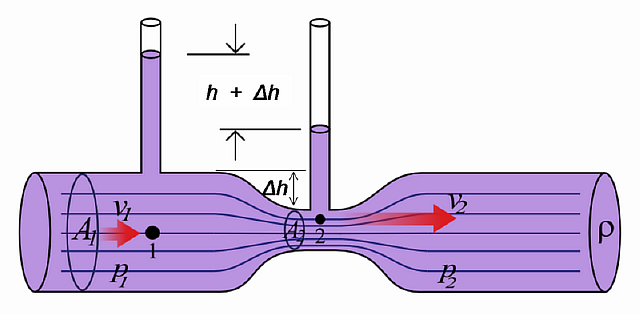
Эффект Вентури хорошо иллюстрируется рисунком, приведенным ниже:
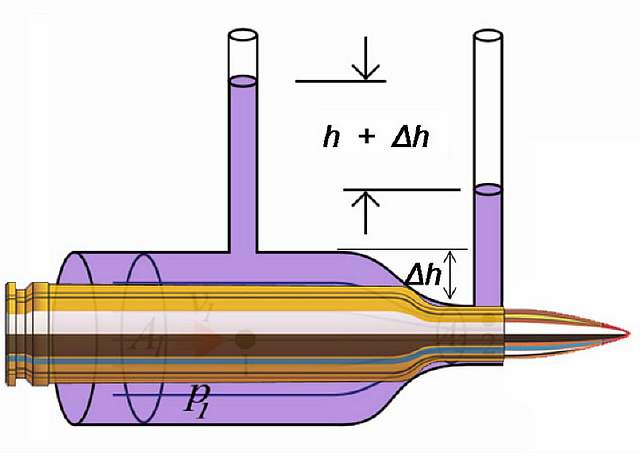
Патроны, спроектированные на использовании эффекта Вентури, увеличивают скорость полёта пули после выстрела. Наложение изображений ниже показывает хороший пример того, как выглядит такой патрон:
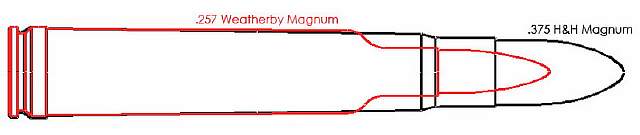
Патрон Weatherby .257 Magnum является одним из лучших примеров применения эффекта Вентури. Этот патрон, разработанный в 1944 году, был не зря разрекламирован как любимый патрон Роя Везерби. Он даёт пуле больше кинетической энергии – и это, в конечном счёте, позволяет поражать мишени на больших расстояниях. Патрон .257 WBY Mag использует гильзу от патрона .375 Holland and Holland. Но его гильза имеет сужение для применения эффекта Вентури (то есть конец под пулю сделан вдвое меньшим по диаметру по сравнению с диаметром гильзы), чтобы соответствовать диаметру пули в 0,257 дюйма.
Малокалиберная пуля с высокой начальной скоростью обеспечивает высокую настильность траектории (в сравнении с патронами .375 H&H дальность прямого выстрела увеличилась на 100 метров), обладает неплохим пробивным действием и значительной убойной силой. Малый импульс отдачи в момент выстрела благоприятно сказывается на кучности и меткости стрельбы, а уменьшение массы патрона позволяет стрелку увеличить носимый боезапас.
Практически полным аналогом патрона Weatherby .257 Magnum надо признать советскую разработку патрона 1974 года под автомат Калашникова калибра 5,45 мм — правда советские конструкторы пошли по пути уменьшения размера гильзы патрона, используя тот же эффект Вентури, с сохранением пробивной силы за счёт головки пули, выполняемой из различных тугоплавких сплавов.


что вы курили когда писали эту статью??? а если гильза будет иметь тот же объем но будет шарообразная, эффекта не будет? а если кубическая? а если такого же диаметра но большей длины? а конусообразная? а конусообразная с обратным склоном конуса, в сторону от пули? при чем тут вообще движение жидкости и твердая пуля? максимум — это движение ГАЗА через канал гильзы и ствола следом за пулей. ну меньше будет давление газа на ствол чем на гильцу (если вообще применимо к такой закрытой конструкци это применять))))
вообще объем гильзы — это количество газа (рабочего тела), а диаметр пули и длина ствола (при такой же длине меньший диаметр приводит к большей длине в калибрах, кстати) — это скорость, с которой пуля вылетит, то есть массу на скорость=импульс. только пули, а не газа или жидкости. энергия, пули, таким образом, зависит всего от 2 компонентов: скорость и масса. меняй их как захочешь. пробивная способность — это давление пули на твердое тело. зависит от площади давления и сили с которой давят. уменьшаем калибр растет давление при той же массе — повышается пробивная способность (при учете достаточной жесткости самой пули, чтобы не растекалась и не плющилась и не крошилась — нужна сталь)
для пробивания нужна большая скорость меньшая площадь (подкалиберные снаряды), для остановки нужна большая площадь (иначе проколет и улетит) — пистолетные пули. снайперу нужна большая дальность и точность — соответственно скорость и масса. большая гильза, тяжелая пуля, длинный ствол.
физику надо в школе хорошо учить а такую дурь не писать…
хотя неплохой тест для школоты в 8-9 классе — учителям физики на заметку как пример псевдонаучной работы.
Не! Это пример американской науки из раздела «английские ученые доказали…» Это просто мы с нашим Советским образованием как то этого недопонимаем.
К стати, сейчас это усиленно внедряют в школах (в смысле амерскую программу обучения и амерские методики). Так что не удивлюсь, что мои дети вполне купятся на такую статейку в будущем. Прискорбно!